Payne的个人小屋

Every day

0%

SQL,何必在忆之一(索引与执行计划篇)

发表于 更新于 分类于 ， Valine：
本文字数： 3.4k 阅读时长 ≈ 3 分钟

B Tree

B树的种类

  • B Tree
  • B+ Tree
  • B* Tree

B 树的定义

B树
（英语：B-tree）是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间
内完成。B树，概括来说是一个一般化的二叉查找树（binary
search
tree）一个节点可以拥有2个以上的子节点。与自平衡二叉查找树
不同，B树适用于读写相对大的数据块的存储系统，例如磁盘。B树减少定位记录时所经历的中间过程，从而加快存取速度。B树这种数据结构可以用来描述外部存储。这种数据结构常被应用在数据库
和文件系统的实现上。

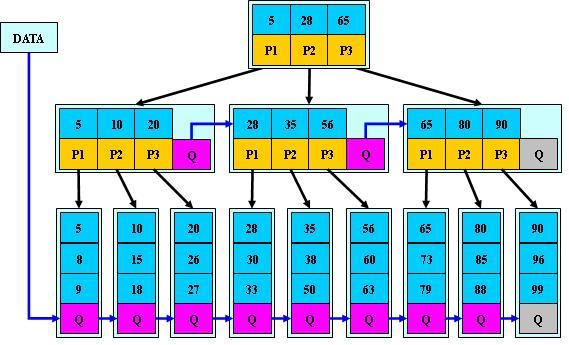
三阶B树如下图所示

采用树形状结构，采用链表进行划分，这样就可以大量减少查询IO(且平均)，以上图为例子，等值的查询，需要三次IO，且仅要三次。

增加、删除、插入、搜索其之间的关系如下表所示

| 算法 | 平均 | 最差 | | :–: | :--------: | :--------: | | 空间 | O(n) | O(
n) | | 搜索 | O(log n) | O(log *
n*) | | 插入 | O(log n) | O(log n) | | 删除 | O(log n) | O(log n) |

B树运用的理念

  • 保持键值有序，以顺序遍历
  • 使用层次化的索引来最小化磁盘读取
  • 使用不完全填充的块来加速插入和删除
  • 通过优雅的遍历算法来保持索引平衡

另外，B树通过保证内部节点至少半满来最小化空间浪费。一棵B树可以处理任意数目的插入和删除。

B树的弊端

  • 除非完全重建数据库，否则无法改变键值的最大长度。这使得许多数据库系统将人名截断到70字符之内。

B+树

B+树是B树的一种变形，比B树具有更广泛的应用，m阶 B+树有如下特征:

  1. 每个结点的关键字个数与孩子个数相等，所有非最下层的内层结点的关键字是对应子树上的最大关键字，最下层内部结点包含了全部关键字.
  2. 除根结点以外，每个内部结点有M/2 到m个孩子.
  3. 所有叶结点在树结构的同一层，并且不含任何信息(可看成是外部结点或查找失败的结点)，因此，树结构总是树高平衡的。

在B+树，这些键值的拷贝被存储在内部节点；键值和记录存储在叶子节点；另外，一个叶子节点可以包含一个指针，指向另一个叶子节点以加速顺序存取。

如图

一颗m阶的B+树和m阶的B_树的差异在于：

1.有n棵子树的结点中含有n个关键字； (而B树是n棵子树有n-1个关键字)

2.所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。(
而B树的叶子节点并没有包括全部需要查找的信息)

3.*所有的非终端结点可以看成是索引部分*，结点中仅含有其子树根结点中最大（或最小）关键字。 (而B
树的非终节点也包含需要查找的有效信息)

B＋树的主要优点：非终端结点仅仅起高层索引作用，而B树非终端结点的关键字除作子树分界外，本身还是实际记录的有效关键字（含记录指针），因此相同的结点空间，B＋树可以设计的阶树比B树大，相同的索引，B＋树的索引层数比B树少，因此检索速度比B树快。此外，B＋树叶子结点包含完整的索引信息，可以较方便地表示文件的稀疏索引。最后，B＋树的检索、插入和删除都在叶子结点进行，比B树相对简单

B+树比B树更适合数据库索引？

1、B+树的磁盘读写代价更低：B+树的内部节点并没有指向关键字具体信息的指针，因此其内部节点相对B树更小，如果把所有同一内部节点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多，一次性读入内存的需要查找的关键字也就越多，相对IO读写次数就降低了。

2、B+树的查询效率更加稳定：由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

3、由于B+树的数据都存储在叶子结点中，分支结点均为索引，方便扫库，只需要扫一遍叶子结点即可，但是B树因为其分支结点同样存储着数据，我们要找到具体的数据，需要进行一次中序遍历按序来扫，所以B+树更加适合在区间查询的情况，所以通常B+树用于数据库索引。

B*树

B树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针；B树定义了非叶子结点关键字个数至少为(
2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）。

B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

B*

树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

小结

B树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；

B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3

这里更加具体的有待探究，欢迎大佬批评与指点

索引

索引的概念

为了更快与查询，例如寻找书中的一页内容，我们可以先从目录进行塞选、从而加快查找的效率

索引的种类(算法)

  • B树索引 --> B+Tree --> B* Tree
  • Hash索引
  • R树
  • Full text
  • GIS

聚簇索引B树结构

区 extend => 簇 => 64 pages -> 1MB

构建前提

  • 建表时，指定了主键列，MySQL InnoDB会将主键作为聚簇索引列，比如 ID NOT NULL Primary Key
  • 如果没有主键,会选择唯一(unique)的列，作为聚集索引.
  • 以上均没有会生成隐藏的聚簇索引

作用

  • 有了聚簇索引后，将插入的数据行，都会按照Id值的顺序，有序在磁盘存储数据

辅助索引B树结构

使用普通的列作为条件构建的索引，需要认为创建

种类

  • 普通的单列辅助索引

  • 联合索引（多个列作为索引条件,生成索引树,理论上设计的好的,可以减少大量的回表查询)

    • 注意最左原则
    • 建立联合索引时，选择重复值少的列。作为最左列

  • 唯一索引（索引列的值都是唯一的.）

作用

优化非聚簇索引列之外的查询优化

构建过程

  1. 索引是基于表中,列(索引键)的值生成的B树结构
  2. 首先提取此列所有的值,进行自动排序
  3. 将排好序的值,均匀的分布到索引树的叶子节点中(16K)
  4. 然后生成此索引键值所对应得后端数据页的指针
  5. 生成枝节点和根节点,根据数据量级和索引键长度,生成合适的索引树高度

前缀索引

当选取的索引列值过长，造成索引树增高，此时我们就需要使用前缀索引

索引管理

什么时候创建索引？

按业务所需创建合适的索引，并不是索引越多越好，将索引建立在经常where\group by\order by\join on
的条件

为什么随意建立索引？

如果冗余索引过多，表的数据发生变化的时候，导致索引频繁更新，造成锁

索引过多会造成优化器选择偏差

1
2
3
4
# 查询表索引
desc table_name
show index from table_name
# PRI 聚簇索引、MUL辅助索引、 UNI索引
1
2
3
4
5
6
7
8
9
10
11
12
13
# 创建索引
create index idx_name1 on city(name);
alter table student add index idx_name(name)

# 联合索引
alter table city add index idx_co_po(countrycode,population);
# 前缀索引
alter table city add index idx_di(district(5));
# 唯一索引
alter table city add unique index idx_uni1(name);

# 删除索引
alter table city drop index Index_Name

小结

  • 聚集索引只能有一个,非空唯一,一般时主键
  • 辅助索引,可以有多个,时配合聚集索引使用的
  • 聚集索引叶子节点,就是磁盘的数据行存储的数据页
  • MySQL是根据聚集索引,组织存储数据,数据存储时就是按照聚集索引的顺序进行存储数据
  • 辅助索引,只会提取索引键值,进行自动排序生成B树结构

建索引原则

1
2
3
4
5
6
(1) 必须要有主键,如果没有可以做为主键条件的列,创建无关列
(2) 经常做为where条件列  order by  group by  join on, distinct 的条件(业务:产品功能+用户行为)
(3) 最好使用唯一值多的列作为索引,如果索引列重复值较多,可以考虑使用联合索引
(4) 列值长度较长的索引列,我们建议使用前缀索引.
(5) 降低索引条目,一方面不要创建没用索引,不常使用的索引清理,percona toolkit(xxxxx)
(6) 索引维护要避开业务繁忙期

关于索引树的高度受什么影响

1
2
3
4
5
6
7
1. 数据量级, 解决方法:分表,分库,分布式
2. 索引列值过长 , 解决方法:前缀索引
3. 数据类型:
变长长度字符串,使用了char,解决方案:变长字符串使用varchar
enum类型的使用enum ('山东','河北','黑龙江','吉林','辽宁','陕西'......)
                                         1      2      3

执行计划获取及分析

执行计划： 优化器按照内置的cost计算，选择执行的方案

cost：IO、CPU、MEM

获取到的是优化器选择完成认为代价最小的执行计划. 作用: 语句执行前,先看执行计划信息,可以有效的防止性能较差的语句带来的性能问题.
如果业务中出现了慢语句，我们也需要借助此命令进行语句的评估，分析优化方案。

select 获取数据的方法

全表扫描(应当尽量避免,因为性能低)

索引扫描

获取不到数据

1
2
3
4
# 查看执行计划
desc 
explain  
# desc(explain) select * from sr_paper

1
2
3
4
5
6
7
8
9
10
11
# 需关注点
table      ：此次查询涉及的表
type      : 查询类型：全表(一般来说有问题，重点关注)、索引(详细探究)
possible_keys  ：可能会用的索引
key       : 最后选择的索引
key_len     ： 索引覆盖长度
rows      : 此次查询需要扫描的行数
Extra      ：额外的信息

# 输出介绍
type： ALL(全表扫描) > index(全索引扫描) > range(索引范围查询) > ref(辅助索引等值查询\非唯一索引扫描) > eq_ref(唯一索引扫描) > const(system)结果只有一条主键或唯一索引扫描

image-20220323231549044

https://www.cnblogs.com/kerrycode/p/9909093.html

相关文章